SAT Math Formulas
The Digital SAT Math Section provides students with a reference sheet containing key formulas. Although we recommend students to know these formulas by heart, it is still reassuring to know that this information will be available during the exam.
Let's go over each of these formulas and when to use them.
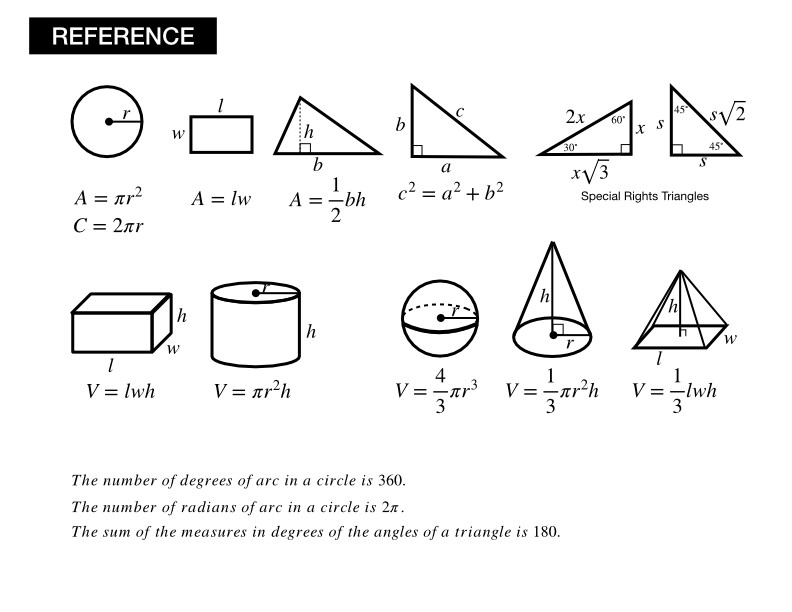
Formulas and Concepts
You might have noticed that all the formulas on the sheet are geometry related, which means that this sheet will only be relevant to geometry and trigonometry problems. There are formulas for areas, volumes and triangle properties.
Unfortunately, this also means that useful formulas for the other topics (such as algebra) on the Math section are not provided, but we still recommend students to study all the formulas useful on the exam, not just these geometry ones.
Circle
The area of a circle is given by the formula where is the radius of the circle. This formula calculates the space enclosed within the circle.
The circumference of a circle is calculated using , which gives the distance around the circle. This is crucial for problems involving the perimeter of circular shapes.
Rectangle
The area of a rectangle is found using , where is the length and is the width. This formula helps determine the amount of space within the rectangle.
Understanding this formula is essential for solving problems related to rectangular plots, rooms, or any scenarios involving rectangular dimensions.
Triangle
The area of a triangle is given by , where is the base and is the height. This formula calculates the space within the triangle.
The sum of the measures in degrees of the angles of a triangle is 180, a fundamental property for solving problems involving triangles.
The Pythagorean Theorem, , is used to find the length of the sides in a right triangle. This is crucial for solving problems involving distances and lengths in geometry.
Special Right Triangles
The 30-60-90 triangle has sides in the ratio , which simplifies many trigonometry problems by providing consistent side ratios.
The 45-45-90 triangle has sides in the ratio , which is useful for problems involving isosceles right triangles.
Rectangular Prism
The volume of a rectangular prism is found using , where is the length, is the width, and is the height. This formula calculates the space within the prism.
This is important for solving problems related to the capacity of boxes, rooms, and other rectangular objects.
Cylinder
The volume of a cylinder is given by , where is the radius of the base and is the height. This formula calculates the space within the cylinder.
This is essential for problems involving cylindrical containers, pipes, and similar objects.
Sphere
The volume of a sphere is calculated using , where is the radius. This formula determines the space within the sphere.
Understanding this formula is crucial for solving problems involving balls, planets, and other spherical objects.
Cone
The volume of a cone is found using , where is the radius of the base and $h$ is the height. This formula calculates the space within the cone.
This is important for problems related to conical containers, ice cream cones, and similar shapes.
Pyramid
The volume of a pyramid is given by , where is the length, is the width, and is the height. This formula calculates the space within the pyramid.
Understanding this formula helps in solving problems related to pyramidal structures and objects.
Arcs and Radians
The number of degrees of arc in a circle is 360, which is essential for problems involving angles and circles.
The number of radians of arc in a circle is , providing an alternative way to measure angles in trigonometry problems.
Reading to put your math skills to the test?
Take a Free Digital SAT Math Practice Module