Mastering Nonlinear Functions Questions on the SAT

Nonlinear functions form a critical component of the SAT math section. This guide covers everything from quadratic to absolute value functions, offering strategies and examples to master these concepts.

Understanding nonlinear functions is an essential skill for any student preparing for the SAT math section. Unlike linear functions, which are straightforward and easier to conceptualize, nonlinear functions introduce many more complexities and strange-looking graphs.

By breaking down these functions into their core components, this guide aims to introduce the various forms of nonlinear functions that can show up on the SAT exam and show students how to solve questions on each type.

1. What is a Nonlinear Function?

Nonlinear functions are functions that have variable rates of change, and they create curves rather than straight lines on a graph. Each type has its unique characteristics and real-world applications, and there are many different types of nonlinear functions that exist.

For the purposes of the digital SAT exam, however, we will focus on the following 4 types:

• Quadratic Functions: Represented as $ax^2 + bx + c$, where a ≠ 0. They form parabolas on a graph.
• Higher-Order Polynomial Functions: Include terms with variables raised to powers higher than two, such as $ax^3 + bx^2 + cx + d$.
• Exponential Functions: Have the form $a \cdot b^x$, where the variable x is in the exponent, leading to rapid increases or decreases.
• Absolute Value Functions: Characterized by the absolute value symbol, producing a V-shaped graph, as in $|x|$.

2. Quadratic Functions

Quadratic functions are represented by the formula $ax^2 + bx + c$, where $a$ is not zero. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the sign of 'a'. Understanding the properties of parabolas is crucial for solving quadratic equations, as it helps in visualizing the solutions and the behavior of the function.

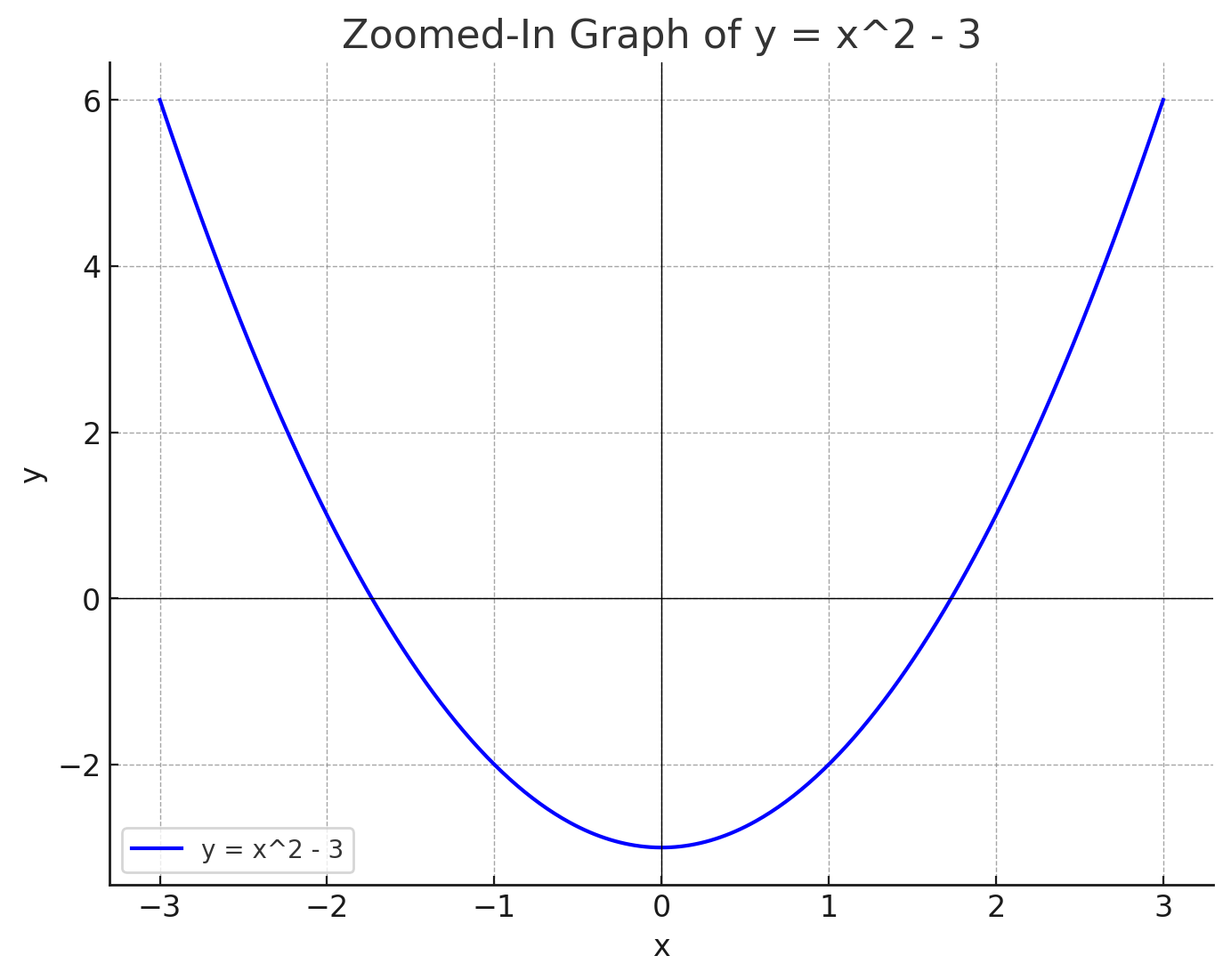
In the context of the SAT, quadratic functions often appear in various forms, including standard, factored, and vertex forms. Each form provides different insights into the function's properties, such as its roots, vertex, and axis of symmetry. The versatility of quadratic functions in modeling real-world scenarios, such as projectile motion and area problems, makes them a recurring theme in SAT questions.

Mastering the methods to solve these equations, including factoring, completing the square, and using the quadratic formula, is essential for success in the math section of the SAT.

Let's consider a detailed example to illustrate the process of solving a quadratic equation:

Given the equation $x^2 - 6x + 8 = 0$ find the values of $x$ that satisfy the equation.

The first step is to determine if the equation can be factored easily. In this case, we look for two numbers that multiply to 8 (the constant term) and add up to -6 (the coefficient of the linear term). These numbers are -4 and -2. Thus, the equation can be factored as $(x - 4)(x - 2) = 0$.

The next step is to set each factor equal to zero and solve for $x$, giving us the roots of the equation. Therefore, the solutions are $x = 4$ and $x = 2$, which are the points where the graph of the quadratic function intersects the x-axis.

3. Higher-Order Polynomial Functions

Higher-order polynomial functions feature variables raised to powers greater than two. These functions can take the form of cubic (third degree), quartic (fourth degree), or even higher degrees.

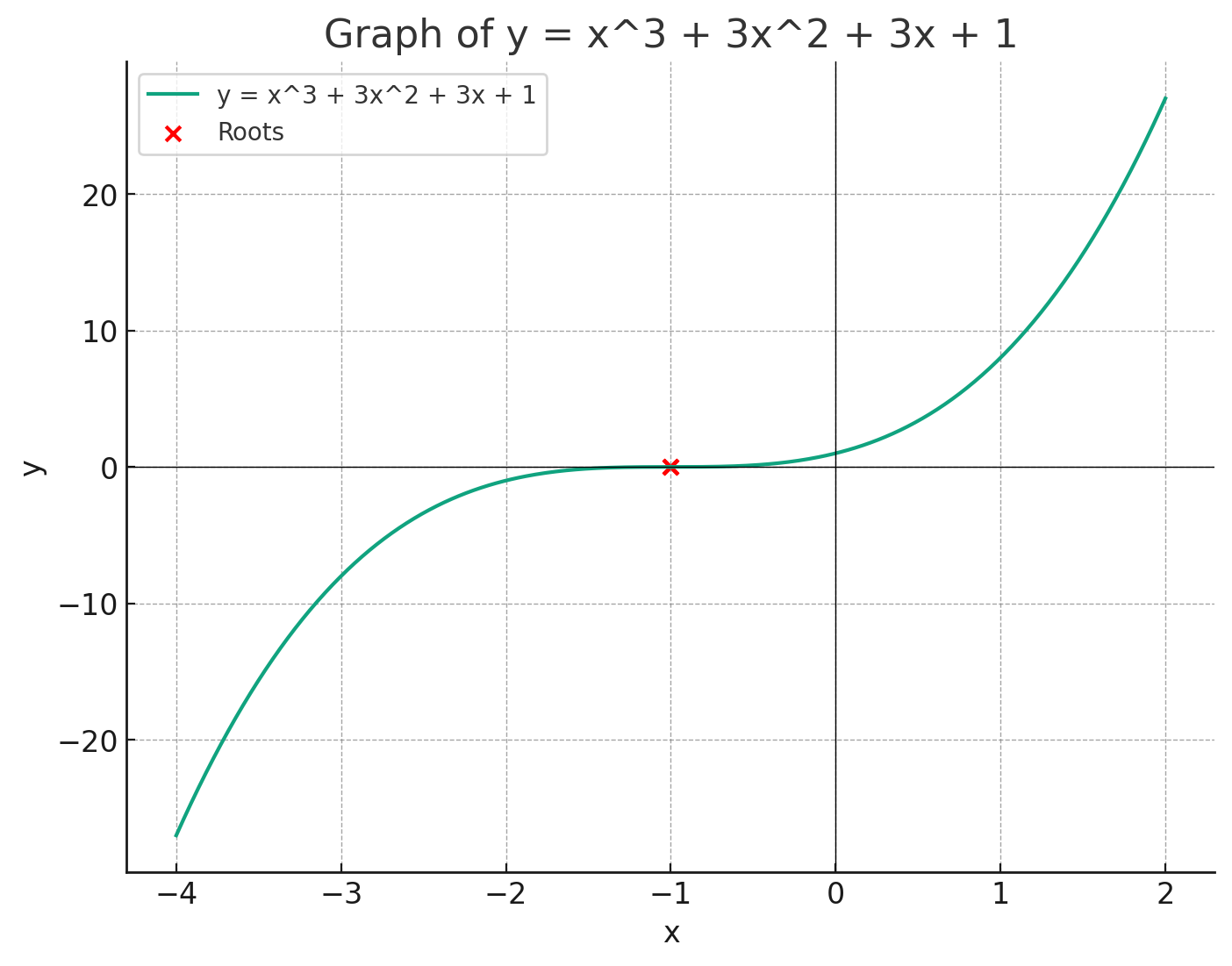
A general form of a higher-order polynomial function is $ax^n + bx^{n-1} + \cdots + k$, where $n$ is the degree of the polynomial, and $a$, $b$, ..., $k$ are constants. The behavior of these functions is more complex than quadratic functions, as they can have multiple turning points and intercepts when graphed.

Solving higher-order polynomial functions on the SAT requires a range of algebraic techniques. Factoring is a common method, though it can be more challenging with higher degrees. When factoring is not feasible, other techniques such as graphical methods may be employed.

Let's explore a detailed example:

Solve the cubic polynomial $f(x) = x^3 - 6x^2 + 11x - 6$.

1. Find a root of the polynomial by inspection or by trying small integer values. For this polynomial, we find that:$f(1) = 1^3 - 6 \cdot 1^2 + 11 \cdot 1 - 6 = 0$, so $x = 1$ is a root.

2. Factor out the root from the polynomial. The factored form becomes:$(x - 1)(x^2 - 5x + 6)$.

3. Factorize the quadratic equation. The fully factored form of the polynomial is:$(x - 1)(x - 3)(x - 2)$.

   Thus, the roots of the polynomial are:$x = 1, x = 3, x = 2$.

4. Exponential Functions

Exponential functions represent a rapid change - either growth or decay. These functions are defined by an equation of the form $a \cdot b^x$, where $a$ is a constant, $b$ is the base of the exponential, and $x$ is the exponent.

What makes exponential functions unique is that the variable ($x$) is in the exponent, leading to faster-than-linear growth or decay. This characteristic is commonly seen in real-world scenarios like population growth, radioactive decay, and compound interest.

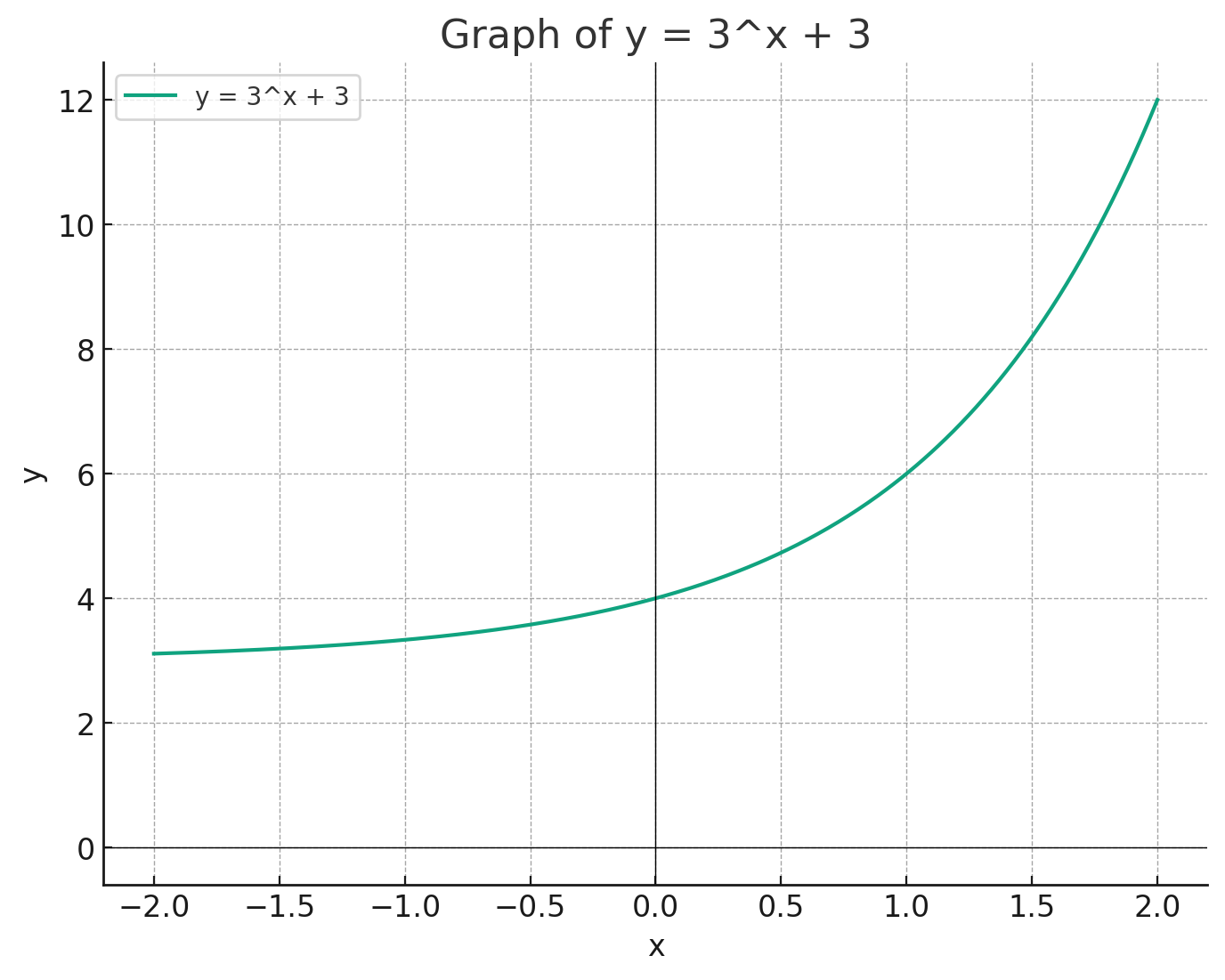
When dealing with exponential functions on the SAT, it's essential to understand their properties, such as the function's rate of change and how it behaves as $x$ increases or decreases.

Solving these functions often involves manipulating the equation to isolate $x$, and recognizing the basic shapes of exponential growth and decay — rapid increase or rapid decrease — is also crucial for solving graph-related questions.

Let’s consider a detailed example:

Solve the equation $3^x = 81$.

The first step is to express both sides of the equation with the same base if possible. In this case, 81 is a power of 3 (since $81 = 3^4$). Therefore, the equation can be rewritten as $3^x = 3^4$. With the bases now equal, the exponents must be equal as well, so we can conclude that $x = 4$. This is a fundamental technique for solving exponential equations, especially when the numbers involved are powers of the same base.

5. Absolute Value Functions

Absolute value functions are a unique type of nonlinear function characterized by their distinctive V-shaped graphs. An absolute value function is defined by an equation of the form $y = |ax + b| + c$, where the absolute value of the linear expression $ax + b$ determines the distance of the value from zero on the number line.

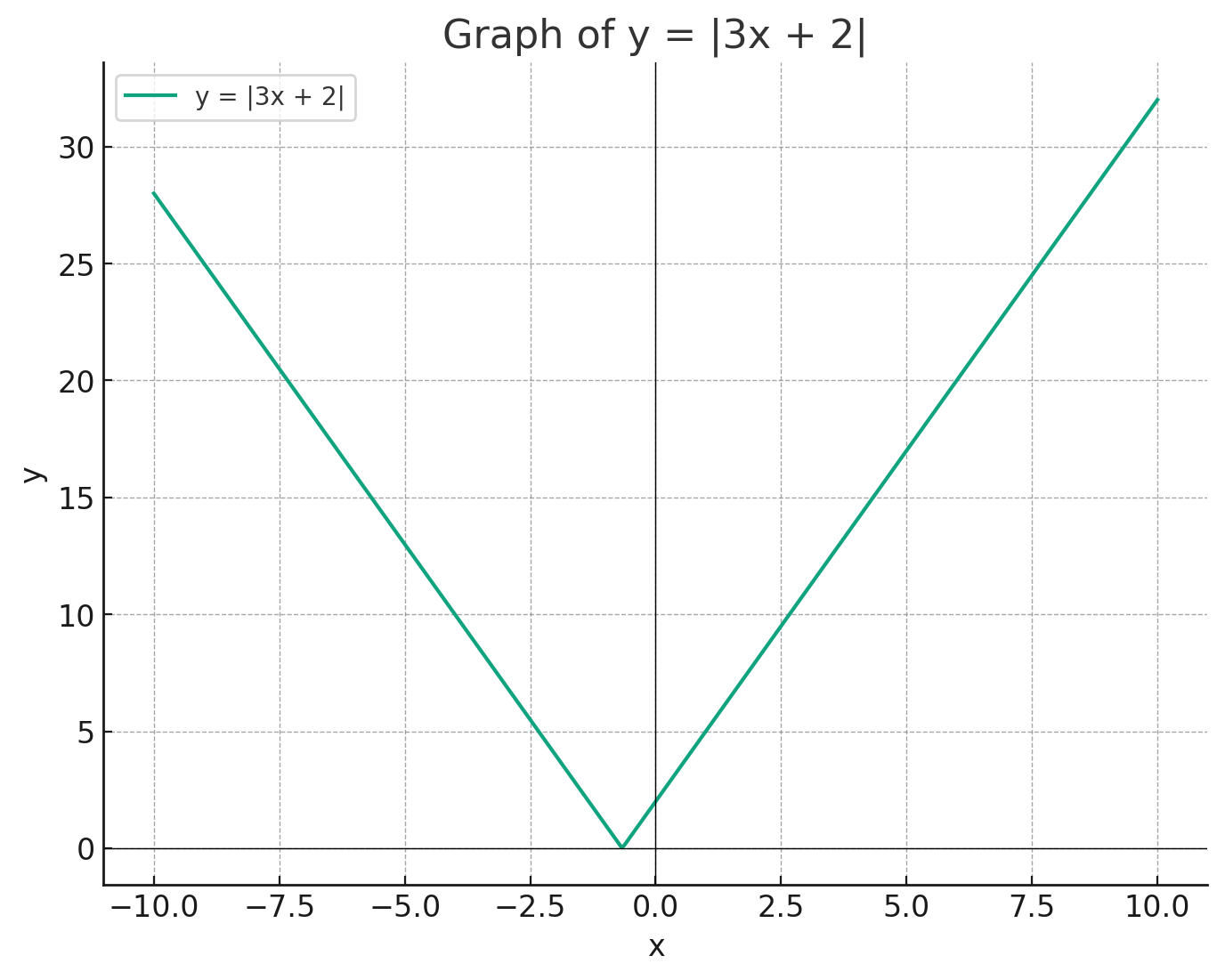
The key feature of these functions is their ability to turn all negative inputs into positive outputs, leading to a graph that mirrors itself across the x-axis or a vertical line.

Solving absolute value equations often involves splitting the equation into two separate cases — one where the expression inside the absolute value is positive, and the other where it is negative. This bifurcation allows for solving each linear equation individually.

Absolute value functions are frequently used in SAT questions to test a student's ability to understand piecewise functions and to solve equations involving absolute values.

For example, consider the equation $|2x - 3| = 7$. To solve it, we split it into two cases: $2x - 3 = 7$ and $2x - 3 = -7$. Solving these linear equations separately, we get $x = 5$ from the first case and $x = -2$ from the second. These solutions represent the points where the graph of the absolute value function intersects the x-axis.

6. Tips and Tricks to Solve Nonlinear Functions Faster

• Understand the Basic Shapes of Graphs: Familiarize yourself with the basic shapes of common nonlinear functions, such as parabolas for quadratic functions, exponential growth and decay, and the V-shape of absolute value functions. Recognizing these shapes aids in quickly identifying the type of function, which is crucial in time-constrained tests like the SAT.

• Practice Factoring Techniques: Mastery in factoring polynomials is key, especially for quadratic and higher-order polynomial functions. Practice different methods of factoring, like grouping, using the quadratic formula, and synthetic division. Efficient factoring can simplify complex problems and save significant time.

• Learn the Properties of Exponents and Logarithms: A solid grasp of the properties of exponents and logarithms is invaluable for exponential functions. Understanding how to manipulate these properties allows for easier equation simplification and variable isolation.

• Use the Substitution Method for Complex Equations: For cumbersome equations, the substitution method can be a powerful tool. This involves replacing part of the equation with a simpler variable, solving for it, and then back-substituting to find the original equation's solution.

• Utilize Graphing Techniques for Understanding Function Behavior: Sketching a quick graph can provide insights into a function's behavior, particularly useful for identifying roots, understanding symmetry, and determining intervals of increase or decrease.