Mastering Trigonometry on the SAT

Trigonometry, often referred to as trig, deals with relationships between the angles and sides of triangles. It involves using right triangles to find missing angle measures and side lengths. In this guide we'll cover the special properties of right triangles, how they related to unit circles, and the core trigonometric functions (sine, cosine, and tangent).

In general trignometry is a fairly advanced topic that can be difficult to understand, and while these questions definitely show up frequently on the SAT there usually aren't more than one or two of them per exam.

So, if you only have a few weeks to study and are not already familiar with trig, we recommend you solidify your understanding of more broad topics such as algebra and nonlinear functions first as those questions show up much more often.

But, if you have the time, trigonometry is definitely worth understanding as it's an essential prerequisite to calculus and college-level math courses.

SOHCAHTOA and the Pythagorean Theorem

First let's begin with the relationship of the three trigonometric functions - sine, cosine and tangent. These functions define the ratio of 2 specific sides of a right triangle relative to one of the angles.

SOHCAHTOA is a well-known mnemonic to remember the relationships between the angles and sides of a right triangle.

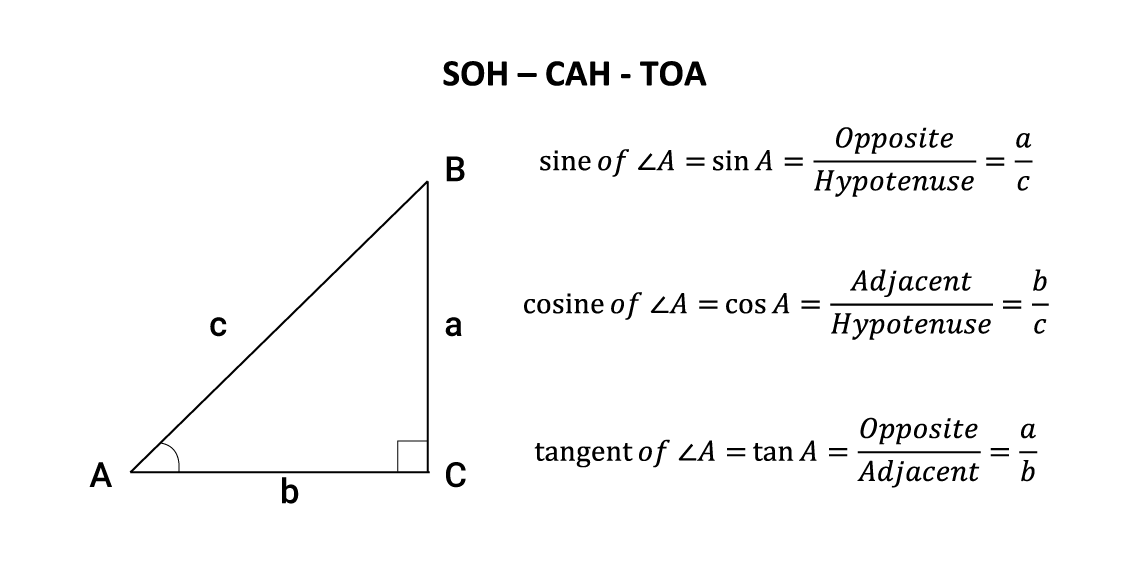
SOH stands for Sine = Opposite/Hypotenuse,
CAH for Cosine = Adjacent/Hypotenuse,
TOA for Tangent = Opposite/Adjacent.

These relationships are the cornerstone of trigonometry and are used to solve for missing sides and angles in right triangles.

To use SOHCAHTOA, you first identify the angle of interest in the triangle. From this angle, you can determine the opposite side, the adjacent side, and the hypotenuse.

For example, if you are given a right triangle with a known angle and one side, you can use one of these trigonometric functions to find the other sides. This is particularly useful in SAT problems where you are asked to find missing dimensions or angles.

Equally as useful is the Pythagorean theorem. Represented as $a^2 + b^2 = c^2$, it is another essential concept in trigonometry as it defines the relationship between the sides of a right triangle. This theorem applies to right triangles (and only right triangles) and states that the sum of the squares of the two legs ($a$ and $b$) is equal to the square of the hypotenuse ($c$).

This relationship is extremely useful for finding the length of one side when the lengths of the other two sides are known. It's also helpful for verifying if a triangle is a right triangle - a triangle with sides that don't satisfy the Pythagorean theorem is not right triangle.

Combining SOHCAHTOA with the Pythagorean theorem allows you to solve a wide range of trigonometric problems. For instance, if you know two sides of a right triangle, you can use the Pythagorean theorem to find the third side and then use SOHCAHTOA to find the angles. This approach is a powerful tool for solving SAT math questions involving right triangles.

Useful formulas for this section:

• $\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}$
• $\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}$
• $\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}$
• $a^2 + b^2 = c^2$

Reciprocal Trigonometric Functions

In addition to sine, cosine, and tangent, there are three reciprocal trigonometric functions: secant (sec), cosecant (csc), and cotangent (cot).

These functions are the reciprocals of cosine, sine, and tangent, respectively. Understanding these reciprocal functions can provide additional tools for solving trigonometric problems.

• $\sec(x) = \frac{1}{\cos(x)}$
• $\csc(x) = \frac{1}{\sin(x)}$
• $\cot(x) = \frac{1}{\tan(x)}$

These reciprocal functions are useful in various trigonometric problems, particularly when dealing with ratios of sides that are not directly given. For example, if you know the sine of an angle, you can easily find the cosecant by taking the reciprocal. This can simplify calculations and provide alternative ways to solve problems.

It's important to remember the relationships between these functions and their reciprocals. For instance, secant corresponds with cosine, cosecant with sine, and cotangent with tangent. Keeping these relationships in mind will help you navigate through trigonometric problems more efficiently - it's very easy to lose precious time on the exam from formula searching!

Trigonometric Identities

Trigonometric identities are equations involving trigonometric functions that hold true for all values of the variable. These identities are powerful tools for simplifying and solving trigonometric problems. Some of the most important identities include the Pythagorean identities, quotient identities, and reciprocal identities.

The Pythagorean identities are derived from the Pythagorean theorem and include:

• $\sin^2(x) + \cos^2(x) = 1$
• $1 + \tan^2(x) = \sec^2(x)$
• $1 + \cot^2(x) = \csc^2(x)$

These identities are useful for converting between different trigonometric functions and for solving equations.

The quotient identities express tangent and cotangent as ratios of sine and cosine:

• $\tan(x) = \frac{\sin(x)}{\cos(x)}$
• $\cot(x) = \frac{\cos(x)}{\sin(x)}$

These identities are helpful for simplifying expressions involving tangent and cotangent.

Reciprocal identities express the reciprocal relationships between trigonometric functions:

• $\sec(x) = \frac{1}{\cos(x)}$
• $\csc(x) = \frac{1}{\sin(x)}$
• $\cot(x) = \frac{1}{\tan(x)}$

These identities are useful for converting between functions and for solving equations involving reciprocals.

Radians

Radians measure angles based on the radius of the circle. One complete revolution around a circle is $2\pi$ radians, equivalent to 360 degrees. Radians provide an alternative way of measuring angles that is often more convenient in advanced mathematics and calculus.

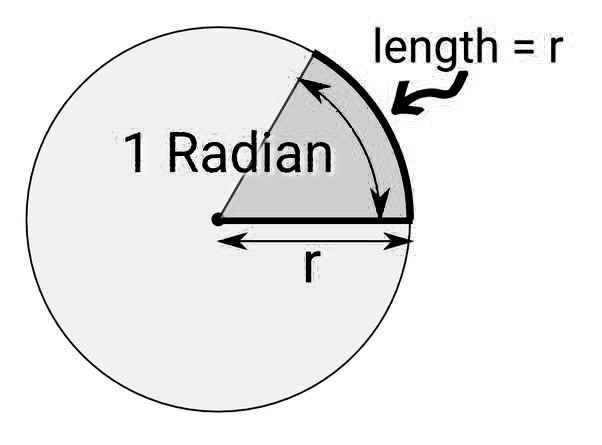
To convert between degrees and radians, use the following formulas:

1) $\text{Degrees} = \text{Radians} \times \frac{180}{\pi}$

2) $\text{Radians} = \text{Degrees} \times \frac{\pi}{180}$

These conversions are essential for solving trigonometric problems where angles are given in different units.

Radians are particularly useful when dealing with the unit circle and trigonometric functions. The unit circle is a circle with a radius of 1, centered at the origin of the coordinate plane. Angles measured in radians correspond directly to the arc length on the unit circle, making calculations more straightforward.

When working with trigonometric functions and the unit circle, it's important to be comfortable with both degrees and radians. Many SAT problems will require you to switch between these units, so practice converting between them and understanding their relationship to the unit circle.

The Unit Circle

The unit circle is a circle with a radius of 1, centered at the origin of the coordinate plane. It allows us to extend trigonometric functions beyond right triangles, providing values for any angle. The equation of the unit circle is $x^2 + y^2 = 1$.

The unit circle provides a way to find the values of trigonometric functions for angles greater than 90 degrees and for negative angles. By extending the right triangle concepts to the unit circle, we can determine the sine, cosine, and tangent of any angle.

To use the unit circle, we find the coordinates of the point where the terminal side of the angle intersects the circle. The x-coordinate corresponds to the cosine of the angle, and the y-coordinate corresponds to the sine of the angle. This method works for all angles, including those in different quadrants.

The unit circle also introduces the concept of reference angles, which are used to find trigonometric values for angles outside the first quadrant.

A reference angle is the acute angle formed between the terminal side of the given angle and the x-axis. By using reference angles and the unit circle, we can find the values of trigonometric functions for any angle.

Useful formulas for this section:

• $x^2 + y^2 = 1$
• $\sin(\theta) = y$
• $\cos(\theta) = x$
• $\tan(\theta) = \frac{y}{x}$

Graphing Trigonometric Functions

Understanding how to graph sine, cosine, and tangent functions is crucial. The graphs of these functions are periodic, repeating every $2\pi$ for sine and cosine, and every $\pi$ for tangent. The standard forms are $y = \sin(x)$, $y = \cos(x)$, and $y = \tan(x)$.

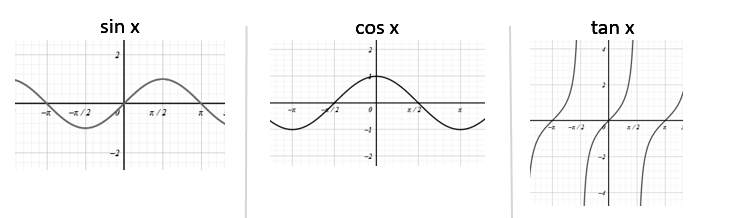
The sine and cosine graphs have a wave-like shape, known as a sinusoidal pattern. The amplitude of the graph is the maximum value of the function, and the period is the length of one complete cycle.

The sine and cosine functions have an amplitude of 1 and a period of $2\pi$. These graphs are important for understanding the behavior of trigonometric functions over different intervals.

The tangent graph, however, is different from the sine and cosine graphs. It has vertical asymptotes where the function is undefined, and it repeats every $\pi$.

The tangent graph has a unique shape, with intervals of increase and decrease separated by the asymptotes. Understanding the tangent graph is essential for solving problems involving tangent functions.

Graphing trigonometric functions also involves understanding transformations, such as shifts, stretches, and reflections. By changing the coefficients and constants in the function's equation, you can modify the graph's shape and position.

For example, $y = A\sin(Bx + C) + D$ represents a transformed sine function, where $A$ affects the amplitude, $B$ affects the period, $C$ affects the horizontal shift, and $D$ affects the vertical shift.

Special Right Triangles

Special right triangles, such as the 30-60-90 and 45-45-90 triangles, have fixed ratios between their sides. These triangles frequently appear on the SAT and can simplify solving problems involving trigonometric functions.

By familiarizing yourself with these special triangles and their properties, you can save time and effort when solving trigonometric problems on the SAT. They also provide a quick and reliable way to determine side lengths and angles, making them valuable tools for test preparation.

30-60-90 Triangle

The 30-60-90 triangle is a special right triangle with angles of 30°, 60°, and 90°. The side lengths are in the ratio 1 : √3 : 2. This means that if the shorter leg (opposite the 30° angle) has a length of $a$, the longer leg (opposite the 60° angle) will have a length of $a√3$, and the hypotenuse will have a length of $2a$.

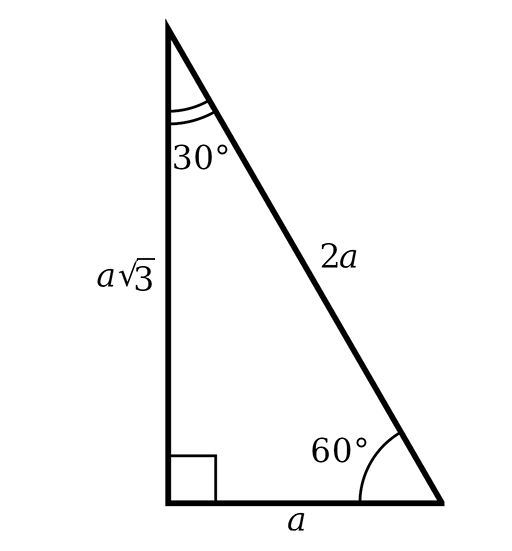
Formulas for a 30-60-90 triangle:

• Shorter leg = $a$
• Longer leg = $a√3$
• Hypotenuse = $2a$

These relationships are useful for quickly finding the lengths of the sides when given one side length. For example, if you know the hypotenuse is 10, you can find the shorter leg by dividing by 2, giving 5, and the longer leg by multiplying the shorter leg by √3, giving $5√3$.

Understanding the properties of the 30-60-90 triangle can save time on the SAT by allowing you to quickly solve problems without needing to use the Pythagorean theorem or trigonometric functions.

45-45-90 Triangle

The 45-45-90 triangle is another special right triangle with angles of 45°, 45°, and 90°. The side lengths are in the ratio 1 : 1 : √2. This means that if one leg has a length of $a$, the other leg will also have a length of $a$, and the hypotenuse will have a length of $a√2$.

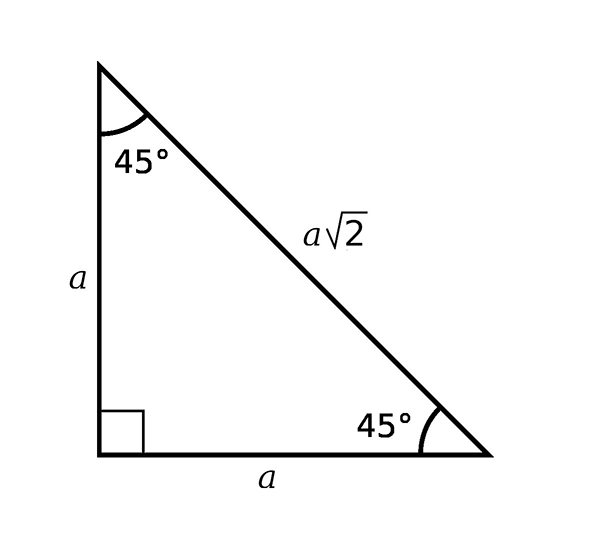
Formulas for a 45-45-90 triangle:

• Legs = $a$
• Hypotenuse = $a√2$

These relationships make it easy to find the lengths of the sides when given one side length. For example, if you know the hypotenuse is 10, you can find the legs by dividing the hypotenuse by √2, giving approximately 7.07.

The 45-45-90 triangle is particularly useful on the SAT for problems involving square and diagonal distances, as these often create 45-45-90 triangles.